If you are so sure that you are right and already “know it all”, why bother and even read this? There is no comment section to argue.

I beg to differ. You utter fool! You created a comment section yourself on lemmy and you are clearly wrong about everything!

You take the mean of 1 and 9 which is 4.5!

/j

I guess if you wrote it out with a different annotation it would be

‎ ‎ 6

-‐--------‐--------------

2(1+2)

=

6

-‐--------‐--------------

2×3

=

6

–‐--------‐--------------

6

=1

I hate the stupid things though

What if the real answer is the friends we made along the way?

Hi! Nice blog post. Since you asked for feedback I’ll point out the one thing I didn’t really understand. You explain the difference between the calculators by showing excerpts from the manuals and you highlight that in the first manual, implicit multiplication is prioritised. But the text you underlined only refers to implicit multiplication involving special expressions(?) like pi, e, sqrt or log, and nothing about “regular” implicit multiplication like 2(1+3). So while your photos of the calculator results are great proof that the two models use a different order of operations, to me the manuals were a bit confusing since they did not actually seem to prove your point for the example math problems you are discussing. Or maybe I missed something?

I think this speaks to why I have a total of 5 years of college and no degree.

Starting at about 7th grade, math class is taught to every single American school child as if they’re going to grow up to become mathematicians. Formal definitions, proofs, long sets of rules for how you manipulate squiggles to become other squiggles that you’re supposed to obey because that’s what the book says.

Early my 7th grade year, my teacher wrote a long string of numbers and operators on the board, something like 6 + 4 - 7 * 8 + 3 / 9. Then told us to work this problem and then say what we came up with. This divided us into two groups: Those who hadn’t learned Order of Operations on our own time who did (six plus four is ten, minus seven is three, times eight is 24, plus three is 27, divided by nine is three) Three, and who were then told we were wrong and stupid, and those who somehow had, who did (seven times eight is 56, three divided by nine is some tiny fraction…) got a very different number, and were told they were right. Terrible method of teaching, because it alienates the students who need to do the learning right off the bat. And this basically set the tone until I dropped out of college for the second time.

I am so glad that nothing I do in life will ever cause this problem to matter to me.

The way I was taught in school, the answer is clearly 1, but I did read the blog post and I understand why that’s actually ambiguous.

Fortunately, I don’t have to care, so will sleep well knowing the answer is 1, and that I’m as correct as anyone else. :-p

What the heck are you all fighting about? It’s BODMAS.

FACT CHECK 3/5

It’s only a matter of taste and how widespread a convention or notation is

The rules are in every high school Maths textbook. The notation for your country is in your country’s Maths textbooks

There are no arguments or proofs about what definition is correct

1+1=2 by definition (or whatever the notation is in your country). If you write 1+1=3 then that is wrong by definition

I found a lot of explanations online that were either half-assed or just plain wrong

And you seem to have included most of them so far - “implicit multiplication”, “weak juxtaposition”, “conventions”, etc.

You either were taught something wrong or you misremember it.

Spoiler alert: It’s always the latter

IMHO the mnemonics would be better without “division” and “subtraction”, because it would force people to think about it before blindly applying something the wrong way – “PEMA” for example. Parentheses, exponentiation, multiplication, addition

In fact what would happen is now people wouldn’t know in what order to do division and subtraction, having removed them from the mnemonic (and there’s absolutely no reason at all to remove them - you can do everything in the mnemonic order and it works, provided you also obey the left-to-right rule, which is there to make sure you obey left associativity)

parenthesis and exponents students typically don’t learn the order of operations through some mnemonics they remember them through exercise

That’s not true at all. Have you not read through some of these arguments? They’re all full of “Use BEDMAS!”, “Use PEMDAS!”, “It’s PEMDAS not BEDMAS!” - quite clearly these people DID learn order of operations through the mnemonics

trying to remember some random acronyms

There’s no requirement to memorise any acronym - you can always just make up your own if you find that easier! I did that a lot in university to remember things during the exam

they also state to “not use × to express a simple product”

…because a product is a Term, and to insert a x would break it into 2 Terms

A product is the result of a multiplication

The center dot also should not be used to mean a simple product

Exact same reason. They are saying “don’t turn 1 term into 2 terms”. To put that into the words that you keep using, “don’t use weak juxtaposition”

Nobody at the American Physical Society (at least I hope) would say that 6/2×3 equals one, because that’s just bonkers

Because it would break the rule of left associativity (i.e. left to right). No-one is advocating “multiplication before division” where it would violate left to right (usually by “multiplication” they’re actually referring to Terms, and yes, you literally always have to do Terms before Division)

÷ (obelus), : (colon) or / (solidus), but that is not the case and they can be used interchangeably without any difference in meaning. There are no widespread conventions, that would attribute different meanings

Yes there is. Some countries use : for divide, whereas other countries use it for ratio

most standards forbid multiple divisions with inline notation, for example expressions like this 12/6/2

Name one! Give me a reference! There’s nothing forbidding that in Maths (though we would more usually write it as 12/(6x2)). Again, all you have to do is obey left to right

Funny enough all the examples that N.J. Lennes list in his letter use

…Terms. Same as all textbooks do now

and thus his rule could be replaced by

…Terms, the already-existing rule that he apparently didn’t know about (he mentions them, and products, but manages to completely miss what that actually means)

“Something, something, distributive property, something ….”

Something, something, Distributive Law (yes, some people use the wrong name, but in talking about the property, not the law, you’re knocking down a strawman)

The distributive property is just a property that applies to some operations

…and The Distributive Law applies to every bracketed term that has a coefficient, in this case it’s 2(1+2)

It has nothing to do with the order of operations

And The Distributive Law has everything to do with order of operations, since solving Brackets is literally the first step!

I’ve no idea where this idea comes from

Maybe you should’ve asked someone. Hint: textbooks/teachers

because there aren’t any primary sources (at least I wasn’t able to find any)

Here it is again, textbook references, proofs, memes, the works

should be calculated (distributed) first

Bingo! Distribution isn’t Multiplication

6÷2(3). If we follow the strong juxtaposition convention, we must

…distribute the 2, always

It has nothing to do with the 3 being inside parentheses

It has everything to do with there being a coefficient to the brackets, the 2

Those parentheses are only there, because

…it’s a factorised term, and the opposite of factorising is The Distributive Law

the parentheses do not force the multiplication

No, it forces distribution of the coefficient. a(b+c)=(ab+ac)

The parentheses are only there to make it clear that

…it is a factorised term subject to The Distributive Law

we are implicitly multiplying two separate numbers.

They’re NOT 2 separate numbers. It’s a single, factorised term, in the same way that 2a is a single term, and in this case a is equal to (1+2)!

With the context that the engineer is trying to calculate the radius of a circle it’s clear that they meant r=C/(2π)

Because 2π is a single term, by definition (it’s the product of a multiplication), as is r itself, so that should actually be written r=(C/2π)

When symbols for quantities are combined in a product of two or more quantities, this combination is indicated in one of the following ways: ab,a b,a⋅b,a×b

Incorrect. Only the first one is a term/product (not separated by any operators) - the last 2 are multiplications, and the 2nd one is literally meaningless. Space isn’t defined as meaning anything in Maths

Division of one quantity by another is indicated in one of the following ways:

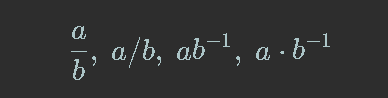
The first is a fraction

The second is a division

The third is also a fraction

The last is a multiplication by a fraction

Creates ambiguity since space isn’t defined to mean anything in Maths. Looks like a typo - was there meant to be a multiply where the space is? Or was there not meant to be a space??

By definition ab^-1=a¹b^-1=(a/b)

deleted by creator

FACT CHECK 5/5

most people just dismiss that, because they “already know” the answer

Maths teachers already know how to do Maths. Huh, who would’ve thought? Next thing you’ll be telling me is English teachers know the rules of grammar and how to spell!

and a two-sentence comment can’t convince them how and why it’s ambiguous

Literally NOTHING can convince a Maths teacher it’s ambiguous - Maths teachers already know all the rules of Maths, and which ones you’re breaking

Why read something if you have nothing to learn about the topic that’s so simple that you know for a fact that you are right

To fact check it for the benefit of others

At this point I hope you understand how and why the original problem is ambiguous

At this point I hope you understand why it isn’t ambiguous. Tip: next time check some Maths textbooks or ask a Maths teacher

that one of the two shouldn’t even be a thing

Neither of them is a thing

not everybody shares your opinion and preferences

Facts you mean. The rules of Maths are facts

There is no mathematically true

There absolutely is! You just chose not to ask any experts about it

the most important thing with this “viral math” expressions is to recognize that

…they are all solvable by following the rules of Maths

One could argue that there should also be a strong connection between coefficients and variables (like in r=C/2π)

There is - The Distributive Law and Terms

it’s fine to stick to “BIDMAS” in school but be aware that that’s not the full story

No, BIDMAS and left to right is the full story

If you encounter such discussions in the wild you could just post a link to this page

No, post a link to this order of operations thread index - it has textbook references, proofs, memes, worked examples, the works!

FACT CHECK 4/5

a solidus (/) shall not be followed by a multiplication sign or a division sign on the same line

There’s absolutely nothing wrong with doing that. The order of operations rules have everything covered. Anything which follows an operator is a separate term. Anything which has a fraction bar or brackets is a single term

most typical programming languages don’t allow omitting the multiplication operator

Because they don’t come with order of operations built-in - the programmer has to implement it (which is why so many e-calculators are wrong)

“.NET IDE0048 – Add parentheses for clarity”

Microsoft has 3 different software packages which get order of operations wrong in 3 different ways, so I wouldn’t be using them as an example! There are multiple rules of Maths they don’t obey (like always rounding up 0.5)

Let’s say we want to clean up and simplify the following statement … o×s×c×(α+β) … by removing the explicit multiplication sign and order the factors alphabetically: cos(α+β) Nobody in their right mind would remove the explicit multiplication sign in this case

This is wrong in so many ways!

1. you did multiplication before brackets, which violates order of operations rules! You didn’t give enough information to solve the brackets - i.e. you left it ambiguous - you can’t just go “oh well, I’ll just do multiplication then”. No, if you can’t solve Brackets then you can’t solve ANYTHING - that is the whole point of the order of oeprations rules. You MUST do brackets FIRST.
2. the term (α+β) doesn’t have a coefficient, so you can’t just randomly decide to give it one. It is a separate term from the rest Is there supposed to be more to this question? Have you made this deliberately ambiguous for example?
3. if the question is just to simplify, then no simplification is possible. You’ve not given any values to substitute for the pronumerals
4. (α+β) is presumably (you’ve left this ambiguous by not defining them) a couple of angles, and if so, why isn’t the brackets preceded by a trig function?
5. As it’s written, it just looks like a straight-forward multiplying and adding pronumerals except you didn’t give us any values for the pronumerals meaning no simplfication is possible
6. if this was meant to be a trig question (again, you’ve left out any information that would indicate this, making it ambiguous) then you wouldn’t use c, o, or s for your pronumerals - you’ve got a whole alphabet left you can use. Appropriate choice of pronumerals is something we teach in Maths. e.g. C for cats, D for dogs. You haven’t defined what ANY of these pronumerals are, leaving it ambiguous

Nobody will interpret cos(α+β) as a multiplication of four factors

7. as originally written it’s 4 terms, not 1 term. i.e. it’s not cos(α+β), it’s actually oxsxxx(α+β), since that can’t be simplified. And yes, that’s 4 terms multiplied!

From those 7 points, we can see this is not a real Maths problem. You deliberately made it ambiguous (didn’t say what any of the pronumerals are) so you could say “Look! Maths is ambiguous!”. In other words, this is a strawman. If you really think Maths is ambiguous, then why didn’t you use a real Maths example to show that? Spoiler alert: #MathsIsNeverAmbiguous hence why you don’t have a real example to illustrate ambiguity

Implicit multiplications of variables with expressions in parentheses can easily be misinterpreted as functions

No they can’t. See previous points. If there is a function, then you have to define what it is. e.g. f(x)=x². If no function has been defined, then f is the pronumeral f of the factorised term f(x), not a function. And also, if there was a function defined, you wouldn’t use f as a pronumeral as well! You have the whole rest of the alphabet left to use. See my point about we teach appropriate choice of pronumerals

So, ambiguity really hides everywhere

No, it really doesn’t. You just literally made up some examples which go against the rules of Maths then claimed “Look! Maths is ambiguous!”. No, it isn’t - the rules of Maths make sure it’s never ambiguous

IMHO it would be smarter to only allow the calculation if the input is unambiguous.

Which is exactly what calculators do! If you type in something invalid (say you were missing a bracket), it would say “syntax error” or something similar

force the user to write explicit multiplications

Are you saying they shouldn’t be allowed to enter factorised terms? If so, why?

force notation that is never ambiguous

We already do

but that would lead to a very convoluted mess that’s hard to read and write

In what way is 6/2(1+2) either convoluted or hard to read? It’s a term divided by a factorised term - simple

providing context that makes it unambiguous

In other words, follow the rules of Maths.

Links about various potentially ambiguous math notations

Spoiler alert: they’re not

“Most ambiguous phrases and notations in maths”

e.g. fx=f(x), which I already addressed. It’s either been defined as a function or as pronumerals, therefore nothing ambiguous

“Absolute value notation is ambiguous”

No, it’s not. |a|b|c| is the absolute value of a, times b, times the absolute value of c… which you would just write as b|ac|. Unlike brackets you can’t have nested absolute values, so the absolute value of (a times the absolute value of b times c) would make no sense, especially since it’s the EXACT same answer as |abc| anyway!

In-line power towers like

Left associativity. i.e. an exponent is associated with the term to its left - solve exponents right to left

People saying “I don’t know how to interpret this” doesn’t mean it’s ambiguous, nor that it isn’t defined. It just means, you know, they need to look it up (or ask a Maths teacher)! If someone says “I don’t know what the word ‘cat’ means”, you don’t suddenly start running around saying “The word ‘cat’ is ambiguous! The word ‘cat’ is ambiguous!” - you just tell them to look it up in a dictionary. In the case of Maths, you look it up in a Maths textbook

Because the actual math is easy almost everybody has an opinion on it

…and any of them which contradict any of the rules of Maths are demonstrably wrong

Most people also don’t know that with weak and strong juxtaposition there are two conflicting conventions available

…and Maths teachers know that both of them are made-up and not real things in Maths

But those mnemonics cover just the basics. The actual real world is way more complicated and messier than “BODMAS”

Nope. The mnemonics plus left to right covers everything you need to know about it

Even people who know about implicit multiplication by juxtaposition dismiss a lot of details

…because it’s not a real thing

Probably because of confirmation bias and/or because they don’t want to invest so much time into thinking about stupid social media posts

…or because they’re a high school Maths teacher and know all the rules of Maths

the actual problem with the ambiguity can’t be explained in a quick comment

Yes it can…

Forgotten rules of Maths - The Distributive Law (e.g. a(b+c)=(ab+ac)) applies to all bracketed Terms, and Terms are separated by operators and joined by grouping symbols

Bam! Done! Explained in a quick comment

I really hate the social media discussion about this. And the comments in the past teached me, there are two different ways of learning math in the world.

I read the whole article. I don’t agree with the notation of the American Physical Society, but who am I to argue that? 😄

I started out thinking I knew how the order of operations worked and ended up with a broader view of the subject. Thank you for opening my mind a bit today. I will be more explicit in my notations from now on.

Having read your article, I contend it should be:
P(arentheses)
E(xponents)
M(ultiplication)D(ivision)
A(ddition)S(ubtraction)
and strong juxtaposition should be thrown out the window.

Why? Well, to be clear, I would prefer one of them die so we can get past this argument that pops up every few years so weak or strong doesn’t matter much to me, and I think weak juxtaposition is more easily taught and more easily supported by PEMDAS. I’m not saying it receives direct support, but rather the lack of instruction has us fall back on what we know as an overarching rule (multiplication and division are equal). Strong juxtaposition has an additional ruling to PEMDAS that specifies this specific case, whereas weak juxtaposition doesn’t need an additional ruling (and I would argue anyone who says otherwise isn’t logically extrapolating from the PEMDAS ruleset). I don’t think the sides are as equal as people pose.

To note, yes, PEMDAS is a teaching tool and yes there are obviously other ways of thinking of math. But do those matter? The mathematical system we currently use will work for any usecase it does currently regardless of the juxtaposition we pick, brackets/parentheses (as well as better ordering of operations when writing them down) can pick up any slack. Weak juxtaposition provides better benefits because it has less rules (and is thusly simpler).

But again, I really don’t care. Just let one die. Kill it, if you have to.

It’s not ambiguous, it’s just that correctly parsing the expression requires more precise application of the order of operations than is typical. It’s unclear, sure. Implicit multiplication having higher precedence is intuitive, sure, but not part of the standard as-written order of operations.